Il Prodotto di Eulero è una formula dimostrata da Leonhard Euler nel 1737,
dove il prodotto del secondo membro dell'uguaglianza percorre tutti i numeri primi.
Questa importante formula mette in relazione una serie in cui compaiono tutti i numeri naturali e un prodotto in cui compaiono tutti i numeri primi.
Esemplificando il prodotto infinito:
ha lo stesso valore della sommatoria della serie:
Più di un secolo dopo Bernhard Riemann nel 1859 utilizzò questa formula per stabilire una relazione tra i suoi zeri e la distribuzione dei numeri primi - Ipotesi di Riemann:
Esemplificando il prodotto infinito:
ha lo stesso valore della sommatoria della serie:
Più di un secolo dopo Bernhard Riemann nel 1859 utilizzò questa formula per stabilire una relazione tra i suoi zeri e la distribuzione dei numeri primi - Ipotesi di Riemann:
le radici non banali si trovano tutte sulla retta descritta dall'equazione s = 1/2 + it , con t numero reale e i unità immaginaria.
http://it.wikipedia.org/wiki/Bernhard_Riemann
http://mathworld.wolfram.com/EulerProduct.html
http://mathworld.wolfram.com/RiemannZetaFunction.html
http://mathworld.wolfram.com/EulerProduct.html
http://mathworld.wolfram.com/RiemannZetaFunction.html
.

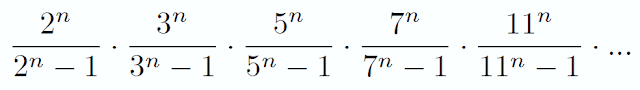


Nessun commento:
Posta un commento