Il "volume" di una ipersfera è dato da:
La "area superficiale" dell'ipersfera è invece data da:

Mentre per la Superficie e':
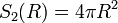
Per la definizione di derivata, come limite del rapporto incrementale, si ottiene che la Superficie e' la derivata del Volume.
E questo in ogni dimensione: D ( Vn ) = Sn-1
Essendo funzioni di potenza, il loro rapporto in ogni dimensione risulta notevolmente semplice:
Vn / Sn-1 = R / n (es. in 3 dim. = R / 3 )
http://en.wikipedia.org/wiki/N-sphere
Nelle formule per il calcolo di Ipervolumi e Ipersuperfici in 2 e 3 dim. compare π, mentre in 4 e 5 dim. π2, in 6 e 7 dim. π3 e così via.
Come esempio per un numero di dimensioni pari si ha:
mentre per numero di dimensioni dispari:
.

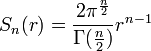
Nessun commento:
Posta un commento