Il calcolo della radice quadrata di un numero e’ abbastanza laborioso.
Può comunque essere effettuato semplicemente, senza l’utilizzo di una calcolatrice, utilizzando lo sviluppo in serie di Taylor della radice di 1+x :
Cominciava così il post 84. Qui di seguito viene mostrato un altro modo per estrarre la radice quadrata che a prima vista può lasciare sorpresi.
Dalla definizione delle medie matematiche (vedi post 200):
Media aritmetica - La media aritmetica viene calcolata sommando tutti i valori a disposizione e dividendo il risultato per il numero dei dati.
Media geometrica - La media geometrica di n termini è la radice n-esima del prodotto degli n valori.
Media
armonica - La media armonica di n termini è definita come il reciproco
della media aritmetica dei reciproci.
In generale si
ha: M aritmetica >
M geometrica > M armonica
Per 2 valori la
media geometrica è medio proporzionale tra le altre 2
M aritmetica : M geometrica = M geometrica : M armonica
e quindi
(M geometrica)2 = M aritmetica x M armonica
Se poi i 2 valori sono abbastanza simili, media aritmetica e media armonica differiscono di poco e per la loro media vale
M geometrica ≈ (M aritmetica + M armonica) / 2
Ad esempio con 9 e 10 si ha:
M aritmetica = 9.5
M armonica = 9.47368
(M aritmetica + M armonica)
/ 2 = 9.48684
M geometrica = 9.48683
In generale,
chiamando i 2 valori x e y, vale
Per l’esempio
precedente
Una decisa semplificazione del calcolo.
Se ora effettuiamo le sostituzioni:
otteniamo la semplice formula:
Basta solo avere l’accortezza di scegliere per z
un numero vicino alla radice che pensiamo di ottenere (non deve essere per
forza intero).
Ad es. la radice quadrata di 80 = 8.94427 è circa (9 + 80/9)/2 = 8.94444
Iterando il
processo 2 o più volte si riesce ad ottenere la precisione voluta, anche
partendo da un valore non scelto con particolare cura.
La formula della radice quadrata può essere estesa alla radice ennesima di un numero N:
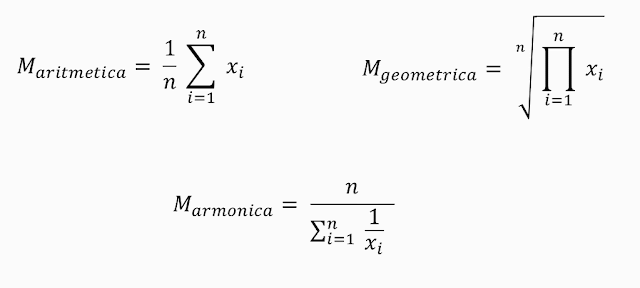




Nessun commento:
Posta un commento