La costante di Gelfond: ep = (-1)-i = 23,14069...
(già vista in “14. Potenze Complesse”) compariva come settimo problema di Hilbert.
La questione era se fosse o meno un numero trascendente.
In seguito si e' dimostrato che la risposta e’ affermativa (Alexander Gelfond, 1934).
In Wikipedia: http://it.wikipedia.org/wiki/Costante_di_Gelfond viene mostrata la proprietà geometrica, che vale per ipersfere di raggio unitario e dimensione pari:
partendo dalla formula per il calcolo del Volume V2n in 2n dimensioni
V2n = pn / n!
S V2n = ep
Più in generale, sostituendo p con p R2 si ottiene:
V2n = pn R2n / n! = ( p R2 )n / n!
S V2n = epR²
che indica la somma dei Volumi di tutte le ipersfere di raggio R e dimensione pari.
In modo meno immediato, usando le “belle serie” del doppio fattoriale riportate in:
si può ricavare la serie che contiene come elementi tutte le formule necessarie per il calcolo dei Volumi delle ipersfere di raggio R in ogni dimensione (!!!):
Questa relazione può anche essere verificata mediante Solve My Math:
Le prime formule per il calcolo di Vn sono ad esempio:
Weisstein, Eric W. "Taylor Series." From MathWorld--A Wolfram Web Resource:
http://mathworld.wolfram.com/TaylorSeries.html
http://mathworld.wolfram.com/UnsolvedProblems.html
23 Problemi di Hilbert (Second International Congress in Paris on August 8, 1900)
http://mathworld.wolfram.com/HilbertsProblems.html
.
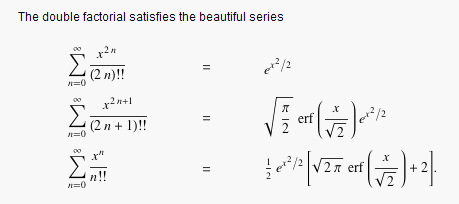



Nessun commento:
Posta un commento