“The complexity for minimum component costs has increased at a rate of
roughly a factor of two per year.”
G.E. Moore,
Elec. Mag., April 1965 (Moore’s Law)
Wikipedia riporta la prima legge di Moore con il seguente enunciato:
« Le prestazioni
dei processori, e il numero di transistor ad esso relativo, raddoppiano ogni 18
mesi. »
Gordon Moore,
cofondatore di Intel con Robert Noyce, all'epoca era a capo del settore R&D
della Fairchild Semiconductor e tre anni dopo fondò l’Intel, scrisse un
articolo su una rivista specializzata nel quale illustrava come nel periodo
1959-1965 il numero di componenti elettronici (ad esempio i transistor) che formano
un chip fosse raddoppiato ogni anno.
Nel 1975 questa previsione si rivelò corretta e prima
della fine del decennio i tempi si allungarono a 2 anni, periodo che rimarrà
valido per tutti gli anni ottanta. La legge, che verrà estesa per tutti gli
anni novanta e resterà valida fino ai nostri giorni, viene riformulata alla
fine degli anni ottanta ed elaborata nella sua forma definitiva, ovvero che le
prestazione dei processori raddoppiano ogni 18 mesi.
"Legge di Moore", Wikipedia, L'enciclopedia libera
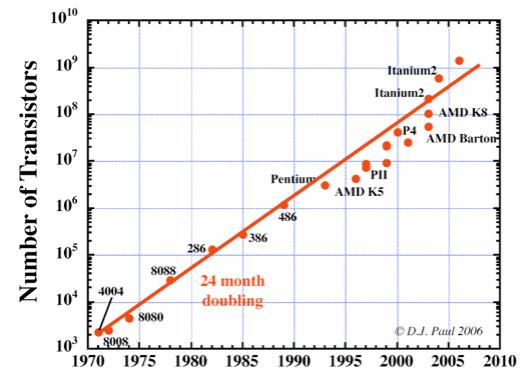 |
| D.J.Paul, University of Cambridge 2006 |
http://www.sp.phy.cam.ac.uk/~SiGe/Moore's%20Law.html
http://it.wikipedia.org/wiki/Legge_di_Moore
Abstract - Moore's law and the computation of Pi
.
Sono contento di vederti così produttivo!
RispondiEliminasbaglio o sono tre post in una settimana?
Comunque, a parte i commenti personali, è interessante notare che l'efficienza raddoppia così rapidamente anche in ambiti PROFONDAMENTE INUTILI come il calcolo delle cifre di PI!
Viene alla mente un commento letto non so più dove, che rimarcava come "30 cifre di pi greco sono sufficienti a calcolare la circonferenza dell'universo visibile, con un errore non rilevabile dal più potente dei microscopi"; da allora (anni '70) universo visibile e microscopi sono cambiati molto, immagino, e forse le cifre necessarie saranno diventate... 40? :D
E se, invece, ci fosse un significato profondo, ma mooolto profondo, anche nelle cifre di pigreco? A questo proposito consiglio a tutti la lettura del bel romanzo di FS "Contact" scritto dal grande Carl Sagan [ne esiste anche una versione cinematografica, ma non mi sembra che riporti anche la parte su pigreco a cui mi riferisco, che è nel finale del libro]
Effettivamente stimando la dimensione dell’Universo dell’ordine di 10^27 metri (o 10^33 micron), si vede che oltre la trentatreesima cifra l’errore commesso nelle misure cosmiche è inferiore al micron.
Elimina