Zibaldone Scientifico: euclide

Visualizzazione post con etichetta euclide. Mostra tutti i post

martedì 10 giugno 2025

273. Formule trigonometriche

La trigonometria è la parte della matematica che studia i triangoli a partire dai loro angoli e lati.

Il compito principale della trigonometria consiste nel calcolare le misure che caratterizzano gli elementi di un triangolo rettangolo (lati, angoli, ecc.) partendo da altre misure note (minimo tre, di cui almeno una lunghezza), per mezzo di speciali funzioni trigonometriche (le più importanti sono seno e coseno).

Le identità trigonometriche sono relazioni fondamentali tra le funzioni.

Le figure che seguono sono “dimostrazioni” delle formule principali, a volte elementari, a volte meno, che potete trovare, ad esempio, in wikimedia commons.

Duplicazione

Somma e sottrazione

Prostaferesi – (S. H. Kung, 1996)

Per queste relazioni rimando direttamente a

Weisstein, Eric W. Prosthaphaeresis Formulas. MathWorld-A Wolfram Web Resource

Come conseguenza del Teorema di Pitagora si ha la nota relazione

sen² α + cos² α = 1

Infine, si riportano 2 esempi interessanti della somma di 3 valori della funzione arcotangente e una dimostrazione del primo teorema di Euclide.

Arctan

Primo teorema di Euclide

Zibaldone Scientifico: 238. Atan

Zibaldone Scientifico: Risultati di ricerca per euclide

lunedì 26 agosto 2024

266. Formule complesse

Il mio amico L. mi ha fatto conoscere questa equazione che mette in relazione le note costanti matematiche e, pi, i, per ricavare un’altra famosa costante:

il numero aureo φ = 1,61803398874989...

Come per l’identità di Eulero, anche in questo caso compaiono contemporaneamente nella stessa formula alcune delle più importanti costanti matematiche.

Per dimostrare la relazione dobbiamo cominciare dalla Sezione Aurea.

Si tratta di dividere un segmento AB in 2 parti (che chiameremo AC e CB) in modo tale che valga la proporzione continua AB : AC = AC : CB

Euclide usò questa formula lavorando sui pentagoni.

Poniamo il segmento più piccolo CB = 1 e AC = x, da cui AB = 1 + x

La condizione richiesta è perciò: (1 + x) / x = x / 1

Quindi si ha x² – x – 1 = 0

Le soluzioni di questa equazione di secondo grado sono:

La Sezione Aurea fu il punto di partenza per lo studio greco dei pentagoni regolari e di tutto ciò che era associato ad essi, come ad esempio il decagono, il dodecaedro e l’icosaedro. Il decagono si può trovare nella base di molte caffettiere.

Come vedremo poi, se si disegna un pentagono regolare di lato 1, allora le diagonali hanno per lunghezza il numero aureo.

Il termine Sezione Aurea è relativamente recente e pare che fu usato per la prima volta da Martin Ohm (fratello del più famoso Georg Simon Ohm che ha dato il nome alla legge) nel suo libro del 1835.

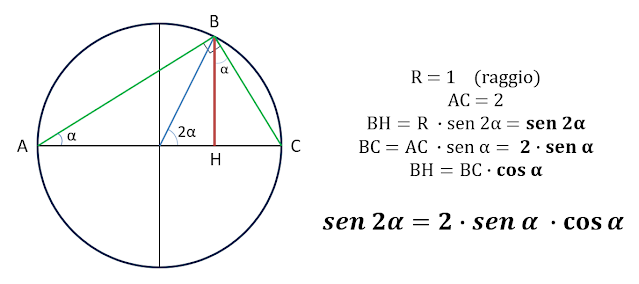
Prima di vedere perché, rivediamo qualche nozione di trigonometria.

La trigonometria studia i triangoli rettangoli a partire dai loro angoli. Il suo compito principale consiste nel calcolare le misure che caratterizzano gli elementi del triangolo (lati, angoli, ecc.) per mezzo di speciali funzioni partendo da misure note.

Le funzioni trigonometriche (le più importanti sono seno e coseno) vengono anche usate in maniera indipendente dalla geometria, ad esempio in connessione con la funzione esponenziale.

1) Il seno di un angolo è il rapporto fra la lunghezza del lato opposto e la lunghezza dell'ipotenusa.

2) Il coseno di un angolo è il rapporto fra la lunghezza del lato adiacente e la lunghezza dell'ipotenusa.

La formula di Eulero è una formula nel campo dell'analisi complessa che mostra una profonda relazione fra le funzioni trigonometriche e la funzione esponenziale complessa. L'identità di Eulero è un caso particolare della formula di Eulero.

La formula di Eulero, dal nome del matematico Leonhard Euler, è stata provata per la prima volta da Roger Cotes nel 1714 e poi riscoperta e resa celebre da Eulero nel 1748. Nessuno dei due vide l'interpretazione geometrica della formula: la visione dei numeri complessi come punti nel piano arrivò solo circa 50 anni dopo, per opera di Wessel, Argand e Gauss.

La dimostrazione più diffusa è basata sullo sviluppo in serie di Taylor della funzione esponenziale.

La formula di Eulero permette anche di interpretare le funzioni seno e coseno come semplici varianti della funzione esponenziale:

formula di Eulero: e^ix = cos x + i sen x

la formula di Eulero permette anche di interpretare le funzioni seno e coseno come semplici varianti della funzione esponenziale:

sen x = ( e^ix - e^-ix ) / 2i cos x = ( e^ix + e^-ix ) / 2

Come noto, gli angoli possono essere espressi in diversi modi, i più utilizzati sono i gradi sessagesimali e i radianti. Di seguito, a seconda dello scopo, verranno presi in considerazione entrambi.

Mostriamo ora alcuni angoli notevoli: 30, 36, 45, 60 e 90 gradi.

In particolare, il seno (30°) = ½ (il cui quadrato è uguale a ¼); in modo analogo i quadrati del seno di 45, 60 e 90 gradi sono rispettivamente: 2/4, 3/4 e 4/4.

Un pentagono regolare di lato 1 (per es. DE) ha invece altre particolari proprietà e si può dimostrare che le diagonali (per es. AD) hanno lunghezza φ.

I 2 triangoli isosceli ADE e DCE sono simili per cui AD : DE = DE : CE

Ponendo AD = x si ha:

x : 1 = 1 : (x – 1) 1 = x² – x x² – x – 1 = 0

Per cui in analogia a quanto visto sopra: AD = φ

cioè, in un pentagono regolare di lato 1, le diagonali sono uguali a φ

Per il triangolo rettangolo ABC si può quindi ricavare:

cos 36° = AB / AC = φ / 2 = 0,809016994374945…

Combinando questo risultato con la funzione per il coseno, si ottiene l’enunciato iniziale:

Riporto in seguito altre formule notevoli:

Zibaldone Scientifico: 89. Ottantanove (zibalsc.blogspot.com)

Zibaldone Scientifico: 90. Ottantanove bis (zibalsc.blogspot.com)

Zibaldone Scientifico: 139. Sezione aurea immaginaria (zibalsc.blogspot.com)

Zibaldone Scientifico: 146. Argomenti Complessi (zibalsc.blogspot.com)

Zibaldone Scientifico: 161. Guarda e dimmi (Look and Say) (zibalsc.blogspot.com)

Zibaldone Scientifico: 177. Ottagoni e Sezione Aurea (zibalsc.blogspot.com)

Zibaldone Scientifico: 228. Quasi (zibalsc.blogspot.com)

Zibaldone Scientifico: 229. Penrose (zibalsc.blogspot.com)

Golden ratio - Wikipedia

Generalizations of Fibonacci numbers - Wikipedia

Formula di De Moivre

Formula di Eulero - Wikipedia

Identità di Eulero

Piano complesso

Radice dell'unità

Rappresentazione dei numeri complessi

Storia dei numeri complessi

Calcinator™ Free Online Mobile Web Scientific Calculator: complex numbers, exponential trigonometric statistics hyperbolic and algebraic functions

lunedì 22 agosto 2016

216. Hilbert’s Hotel

Prima o poi, in un blog che si rispetti, si deve parlare di questo paradosso. E visto che ci sono molti blog degni di rispetto, basta scrivere su un motore di ricerca alcune parole chiave, per trovare un’infinità di post che parlano di questi argomenti. Quel che faremo qui è di esporre i diversi approcci utilizzati per risolvere brillantemente le varie situazioni che si presentano di volta in volta.

http://www.delcampe.net/

Immaginate un hotel (che chiameremo hotel di Hilbert) con infinite stanze tutte occupate.

Caso 1 - Arriva un nuovo cliente. L’arguto albergatore pensa: non c’è problema; metto il nuovo ospite nella stanza che desidera e sposto nella stanza successiva alla loro tutti gli occupanti delle varie stanze. In questo semplice esempio, se il nuovo ospite sceglie la stanza numero 1, basterà spostare l'ospite della 1 nella 2, quello della 2 nella 3, ecc.; essendo un hotel infinito è possibile trovare una soluzione.

Caso 2 - Dopo un’ora arriva un autobus con infiniti nuovi ospiti. L’arguto albergatore pensa: basta spostare ogni ospite nella stanza con numero doppio rispetto a quello attuale (dalla 1 alla 2, dalla 2 alla 4, ecc.), lasciando ai nuovi arrivi tutte le camere con i numeri dispari, che sono anche esse infinite. Problema risolto.

Ma non è finita qui.

Caso 3 - Il giorno dopo arrivano infiniti autobus (tutti numerati) ed ognuno di questi contiene infiniti passeggeri (che siedono su sedili anch’essi numerati).

A questo punto la faccenda sembra farsi complicata, ma anche in questo caso esiste una soluzione, anzi esistono almeno 5 modi diversi di risolvere la questione:

Modo 1

Che i numeri primi siano infiniti, fu dimostrato da Euclide in una delle più belle dimostrazioni matematiche, e non è complicato rendersi conto che qualsiasi potenza di un primo è divisibile solo per il numero primo stesso. Per cui se poniamo i clienti attualmente residenti nelle camere con numero uguale alle potenze di 2 e i vari autobus in quelle corrispondenti alle potenze dei successivi primi. Cioè, indicando con k il numero della stanza o del sedile occupato, basta seguire questa semplice regola:

ospiti residenti andranno nella camera 2^k es. da camera 7 a camera 128
primo autobus andranno nella camera 3^k es. da posto 4 a camera 81
secondo autobus andranno nella camera 5^k es. da posto 3 a camera 125
terzo autobus andranno nella camera 7^k es. da posto 5 a camera 16807

Questo modo ha il difetto di lasciare libere troppe camere. Ad esempio: 6, 10 e tutte le camere scomponibili in numeri primi differenti, non saranno occupate.

Modo 2

Nel libro “La piccola bottega delle curiosità matematiche del professor Stewart” viene suggerito di iterare il procedimento utilizzato in precedenza per sistemare un solo autobus, per ogni autobus che si deve sistemare. L’inconveniente in questo caso è che ogni ospite dovrà continuare a spostarsi.

Modo 3

Posto k, autobus j, va in 2^j(2k -1)

residenti, vanno nella camera 2⁰ (2k -1) es. da camera 7 a camera 13
primo bus, vanno nella camera 2¹ (2k -1) es. da posto 4 a camera 14
secondo bus, vanno nella camera 2² (2k -1) es. da posto 3 a camera 20
terzo bus, vanno nella camera 2⁴ (2k -1) es. da posto 5 a camera 144

Modo 4

Immaginiamo l’hotel di Hilbert come un classico hotel (ma infinito). Le infinite camere k sono posizionate lungo gli infiniti corridoi j e in infiniti livelli (o piani) p (immaginate un cubo infinito). Possiamo anche complicare ulteriormente la questione, cioè pensare che arrivino infinite persone, su infiniti autobus e per infiniti giorni. Basterà dire loro di recarsi nel corridoio corrispondente al numero del loro autobus, al livello relativo al giorno e applicare il caso 2 visto in precedenza.

Esempio: il primo giorno, il quarto passeggero del terzo autobus, andrà a sistemarsi nella camera numero 7, del terzo corridoio (III), al livello 1 (corridoio giallo).

Modo 5

Per diagonali, utilizzato nella pagina di Wikipedia: “Paradosso del Grand Hotel di Hilbert”. Il metodo si capisce subito osservando l’illustrazione riportata nel post messicano: http://masciencia.org/blog/bienvenidos-al-hotel-hilbert

Il celebre paradosso del Grand Hotel è stato inventato dal grande matematico David Hilbert negli anni ’20 e, come commentato in Wikipedia: “Questo paradosso, nonostante sia piuttosto elementare, ha contribuito, all'epoca ai matematici, ed oggi ai profani, a far comprendere la differenza profonda e sostanziale tra gli insiemi finiti e infiniti…”.

Come detto all’inizio, esistono molti post che parlano di questo paradosso e sono presenti in rete anche molti interessanti video come questo di Jeff Dekofsky:

https://youtu.be/Uj3_KqkI9Zo

http://math.stackexchange.com/questions/286282/hilbert-hotel-what-if-countably-many-buses-each-with-countably-many-guests-arri

https://en.wikipedia.org/wiki/Hilbert%27s_paradox_of_the_Grand_Hotel

http://masciencia.org/blog/bienvenidos-al-hotel-hilbert

http://www.infinitoteatrodelcosmo.it/2016/05/22/gli-infiniti-di-cantor-parte-settima-la-cardinalitadi-q-e-le-diagonali-di-cantor/

domenica 5 luglio 2015

191. La Curvatura degli Ombrelloni

Se le persone credono che la matematica non sia semplice, è soltanto perché non si rendono conto di quanto la vita sia complicata.

John von Neumann

La matematica è una scienza a buon mercato. A differenza della fisica o della chimica, non richiede di particolari attrezzature, basta osservare ciò che ci sta intorno, e qualche cosa su cui congetturare si trova sempre.

Dopo la sosta al bar, sono andato in spiaggia e una delle prime cose che ho notato è stata la particolare forma degli ombrelloni.

E’ da diversi anni che volevo scrivere un post sulla loro forma e questi ultimi mi hanno proprio fornito lo spunto che cercavo.

Claude Perrault (1613-1688) è stato un medico (di professione) e architetto (per diletto) francese. Morì per un'infezione contratta dopo aver sezionato un cammello.

Malgrado si ritenesse un architetto dilettante, a lui si deve la facciata est del Louvre di Parigi.

Terzo in una famiglia di sette figli, ebbe una formazione enciclopedica, con la naturale curiosità e lo spirito critico dello scienziato.

Il fratello Charles fu uno scrittore, autore del celebre libro di fiabe Contes de ma mère l'Oye (it. I racconti di Mamma Oca), raccolta di undici fiabe fra cui Cappuccetto Rosso, Barbablù, La bella addormentata, Pollicino, Cenerentola e Il gatto con gli stivali.

Uno dei problemi che si pose Claude Perrault, giocando con il suo orologio da taschino posto sul tavolo e provando a trascinarlo per la catenella fu:

se trasciniamo un oggetto posto su un piano orizzontale con una corda, quale sarà il percorso dell’oggetto se l’altro capo scorre lungo una linea retta situata sullo stesso piano?

Non riuscendo a risolvere il problema, lo pose quindi all'amico Leibniz (1646-1716) all'epoca del suo soggiorno a Parigi (1672-1676), la soluzione che consiste nella determinazione della curva, venne pubblicata nel settembre del 1693.

La proprietà geometrica caratteristica della curva, è dunque che, in ogni suo punto, il segmento di tangente compreso tra il punto stesso e la retta fissa ha lunghezza costante uguale alla lunghezza della corda. Da tale proprietà se ne deduce l'equazione differenziale.

Per essere precisi, Leibniz cominciò a studiare la curva del moto, ma fu Huygens che riuscì a definirla con precisione. La curva venne chiamata Trattrice (dal latino tractrix, che deriva a sua volta da trahere, trainare).

Una sua proprietà è di avere come evoluta una Catenaria.

Trattrice con oggetto posizionato inizialmente nel punto (4,0)

L’area compresa tra la Trattrice (con lunghezza L della corda) e il suo asintoto è:

La rotazione della Trattrice intorno al proprio asintoto genera la Pseudosfera, che deve il nome al fatto che la sua curvatura è costante in ogni punto e opposta a quella della Sfera:

k = -1/L²

Tale superficie fu proposta da Eugenio Beltrami (1835-1900) come modello di geometria iperbolica nel 1868.

Essa, infatti, localmente soddisfa gli assiomi della geometria iperbolica, allo stesso modo di come la superficie di un Cilindro localmente è un modello equivalente ad un piano euclideo o la Sfera uno di geometria ellittica.

E’ importante sottolineare che la Pseudosfera possiede una curvatura negativa costante, cioè, in maniera analoga alla Sfera (anche se meno evidente), in ogni suo punto si ha lo stesso valore di curvatura.

Un altro esempio è la superficie di Dini che può essere vista come una "torsione" della Pseudosfera. Più precisamente, è una superficie ottenuta assegnando a una Trattrice un moto elicoidale intorno alla propria retta caratteristica. È quindi una superficie elicoidale. Per confronto, la Pseudosfera è ottenuta facendo ruotare una Trattrice intorno alla propria retta caratteristica, ed è quindi una superficie di rotazione.
Come la Pseudosfera, la superficie di Dini ha curvatura gaussiana costante negativa.

Superficie e Volume della Pseudosfera sono rispettivamente:

Per la sfera invece si ha (come noto):

La geometria piana di Euclide si basa su 5 postulati.

Il più famoso di questi è il quinto postulato:

“per un punto esterno ad una retta, si può condurre una sola parallela alla retta”.

Senza entrare nei dettagli, possiamo dire che se non si accetta il quinto postulato, si hanno 2 alternative, alle quali corrispondono 2 diverse geometrie non euclidee:

1. “non si può condurre alcuna parallela” (geometria ellittica)

2. “si possono condurre almeno 2 rette parallele” (geometria iperbolica)

Si distinguono 2 tipi essenziali di curvatura:

· curvatura estrinseca: è la curvatura posseduta dall'oggetto in relazione ad uno spazio piatto di dimensione superiore in cui è immerso e determinabile solo confrontando elementi dell'oggetto in relazione ad elementi dello spazio contenitore;

· curvatura intrinseca: è la curvatura determinabile utilizzando solo operazioni eseguite su elementi dell'oggetto medesimo.

Un esempio di curvatura estrinseca è quella di una superficie cilindrica nello spazio tridimensionale: le linee tracciate sul cilindro sono curve se confrontate con le rette dello spazio in cui il cilindro è immerso. La geometria intrinseca del Cilindro è invece piatta, in quanto su di essa valgono tutti gli assiomi del piano euclideo.

Come si è detto, un Cilindro ha curvatura intrinseca nulla.

ANDY WARHOL, Campbell’s Soup II, 1969, screenprint on woven paper, 88.9 × 58.4 cm. Copyright the Andy Warhol Foundation for the Visual Arts. Courtesy the Andy Warhol Museum, Pittsburgh.

Questo può essere facilmente compreso, pensando che una etichetta di un barattolo non è altro che un foglio rettangolare arrotolato.

http://artasiapacific.com/Magazine/82/TheLittleCanThatCould

Una Sfera ha invece una curvatura intrinseca, determinabile rimanendo all'interno della superficie stessa: sulla Terra, un percorso che parte dal polo nord scendendo lungo un meridiano, ruota ad angolo retto lungo un parallelo e nuovamente ad angolo retto lungo un altro meridiano, ritorna al punto di partenza.

Mentre un percorso analogo eseguito su un piano non ripassa per lo stesso punto.

Tornando all’ombrellone, possiamo provare a scomporlo in figure geometriche semplici; procedendo dal basso verso l’alto avremo così:

· il telo giallo costituente la parte più importante, che può essere pensato come una calotta sferica, la cui curvatura è quindi positiva

· il secondo telo che sembra riprodurre una Pseudosfera (curvatura negativa)

· a seguire una parte cilindrica, una pseudosferica e una sferica.

Si vede quindi che nello stesso oggetto si possono trovare diverse tipologie di superfici.

http://www.vialattea.net/curvatura/index.html

Un altro modo per descrivere la Trattrice, è quella di considerare un cane che viene trascinato dal suo padrone tramite un guinzaglio, lungo un percorso rettilineo: il cane percorrerà una Trattrice.