Zibaldone Scientifico: luglio 2015

domenica 26 luglio 2015

193. Azoto

E’ estate, una calda estate. E allora fa sempre piacere uscire a prendere un po’ d’aria e può capitare di chiedersi perché quest’aria ha una certa composizione e così tanto Azoto.

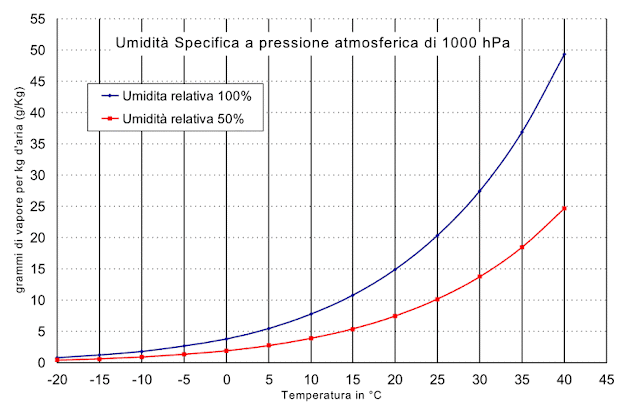
Oppure, in una di queste giornate dove il tasso di umidità è al limite della sopportazione, di pensare a quale sia la percentuale di vapore acqueo e quanta acqua può venir “prodotta” da un condizionatore.

Nel post 93. Clorofilla ed Emoglobina si sono prese in considerazione le abbondanze degli elementi chimici nell’Universo, nella crosta terrestre, nell’acqua di mare e nel corpo umano.

La crosta terrestre è l’unica dove l’Ossigeno è al primo posto (47%) e il Silicio al secondo (28%); negli altri casi è sempre l’Idrogeno il più abbondante e il Silicio si trova solo nella crosta terrestre.

Dell’Azoto si ha qualche traccia significativa solo nel corpo umano.

Se ora prendiamo in considerazione l’atmosfera terrestre abbiamo una situazione ancora una volta completamente differente:

l’aria è composta dal 78,1% di Azoto, dal 20,9% di Ossigeno, dallo 0,95% di Argon ed in percentuali sempre inferiori:

Anidride Carbonica, Neon, Elio, Metano, Krypton, Idrogeno, ecc.

Leonardo da Vinci definiva l’atmosfera una specie di fluido pesante, compressibile e resistente, che avvolge la sfera della terra e dell'acqua; il peso e la pressione che essa esercita su tutti i corpi alla superficie della Terra furono riconosciuti da Galileo Galilei.

Il vapore acqueo nell'aria è di solito meno dell'1% in volume, ma può raggiungere il 4% nei climi umidi; è ovvio che la quantità di vapor d'acqua saturo presente nell'aria dipende dalla temperatura.

Attenzione: quando parliamo di vapore acqueo, non stiamo prendendo in considerazione le nuvole… In meteorologia una nuvola è costituita da minute particelle d'acqua condensata e/o cristalli di ghiaccio, sospese per galleggiamento nell'atmosfera e solitamente non a contatto con il suolo.

Nell'antichità erano conosciuti solo pochi elementi: Carbonio, Oro, Argento, Rame, Zolfo, Stagno, Piombo, Mercurio, Antimonio e Ferro; mentre Arsenico e Zinco erano note prima del XV secolo; infine, all’epoca della rivoluzione francese erano conosciuti (in ordine di scoperta):

Fosforo 1669

Cobalto 1737

Platino 1748

Nichel 1751

Bismuto 1753

Idrogeno 1766

Azoto 1772

Cloro 1774

Manganese 1774

Ossigeno 1774

Molibdeno 1782

Tellurio 1783

Tungsteno 1783

https://en.wikipedia.org/wiki/Abundance_of_the_chemical_elements

https://en.wikipedia.org/wiki/Timeline_of_chemical_element_discoveries

Elementi chimici noti nel 1790

Il rame è forse il più antico metallo conosciuto, così importante da dare il nome ad un periodo durato diversi millenni: l’età del rame.

L'età del bronzo indica invece il periodo successivo caratterizzato dall'utilizzo sistematico ed esteso della metallurgia del bronzo che, per quanto riguarda l'Europa, si estende dal 3500 a.C. al 1200 a.C. circa.

Il termine bronzo identifica la lega rame/stagno.

Tornando ad Azoto e Ossigeno, questi furono identificati all’incirca nello stesso periodo 1772 e 1774.

Daniel Rutherford chiamò l’Azoto “aria nociva”, mentre altri lo soprannominarono “aria bruciata”. Antoine Lavoisier (padre della chimica moderna) gli diede il nome di Azoto (dal greco azotos, senza vita).

Il nome inglese Nitrogen significa “formante nitro” e deriva dal fatto che il nitrato di potassio (sale di potassio dell'acido nitrico, comunemente noto anche con il nome di salnitro o nitro) è un minerale comune che contiene Azoto.

La risposta al perché l’Azoto sia l’elemento principale dell’aria con 4 parti su 5 si può trovare nelle seguenti argomentazioni:

o è un gas volatile

o e’ inerte con i materiali che compongono la crosta terrestre

o e’ molto stabile in presenza di radiazione solare

Nella composizione dell’Universo, Ossigeno e Azoto hanno all’incirca la stessa percentuale (anche se insieme arrivano solo all’1%), ma l’Ossigeno è sicuramente meno inerte dell’Azoto (come riportato sopra, dove si può notare quanto Ossigeno ci sia nella crosta terrestre).

L’Azoto è un gas inerte, in condizioni opportune ha la fondamentale funzione di fertilizzare il suolo, ed è indispensabile ai vegetali quanto la vitamina C lo è per noi. Raramente reagisce con altre sostanze e la difficoltà di farlo partecipare a reazioni importanti lo rese una delle sostanze più studiate da diverse generazioni di chimici.

Per "catturare" l’Azoto si procede in questo modo:

o   si porta il gas ad alte temperature
o   lo si mette a contatto con l’idrogeno
o   si aumenta la pressione a centinaia di atmosfere
o   si aggiunge l’Osmio che funge da catalizzatore

A questo punto l’aria si è trasformata in Ammoniaca, NH₃.

Questa sostanza viene utilizzata per molti scopi ed è alla base di tutti i fertilizzanti.

L’Azoto liquefa a 77,35 K (−195,82 °C) e solidifica a 63,14 K (−210,03 °C).

Se liquefassimo l’aria di un appartamento medio, otterremmo circa 400 litri di Azoto liquido, mentre l’acqua raccolta dipende dalla percentuale dell’umidità e dalla temperatura:

Con una temperatura che supera i 30 gradi e percentuali di umidità dell’ordine dell’80%, si potrebbero avere tra i 5 e i 10 litri d’acqua (senza considerare l’apporto dato da esseri umani e animali presenti).

Malgrado la sua particolare attitudine di gas inerte, l’Azoto è presente in molte sostanze. In natura come nitrato di Potassio KNO₃ (salnitro) e nitrato di Sodio NaNO₃ (nitro del Cile). E’ un costituente di proteine e acidi nucleici.

I più importanti ossidi di Azoto sono il monossido NO e il diossido NO₂.

Non è possibile elencare tutte le sostanze in cui è presente l’Azoto e mi limiterò ad alcune delle più note:

Acido nitrico HNO₃ (con l’acido cloridrico forma l’acqua regia)

Cianuro CN^-

Nicotina C₁₀H₁₄N₂

Trinitrotoluene CH₃C₆H₂(NO₂)₃ (noto anche come tritolo o TNT)

Nitroglicerina C₃H₅(ONO₂)₃

Inoltre: Caffeina, Morfina, Serotonina, Adrenalina, Idrazina, ecc.

http://venus.unive.it/miche/cicli_ecosis/0033.htm

https://en.wikipedia.org/wiki/Timeline_of_chemical_element_discoveries
http://www.nobelprize.org/nobel_prizes/chemistry/laureates/1918/
http://zibalsc.blogspot.it/2014/06/153-acqua-ed-aria.html

domenica 12 luglio 2015

192. I Fiori di Avatar

Nel precedente post, si è visto che la superficie di Dini (come la Pseudosfera) possiede l’interessante caratteristica di avere una curvatura negativa costante e può essere creata con la "torsione" della Pseudosfera.

Più precisamente, è una superficie ottenuta assegnando ad una Trattrice un moto elicoidale intorno alla propria retta caratteristica:

Per confronto, la Pseudosfera è ottenuta facendo ruotare una Trattrice intorno alla propria retta caratteristica.

Ulisse Dini descrisse la superficie con le seguenti equazioni parametriche:

A volte, raccontando le proprie idee si finisce per capirle meglio. Ed è stato così che, dopo una chiacchierata, il mio vicino di scrivania ha notato come la superficie di Dini sembri proprio essere stata presa come modello matematico per disegnare i fiori del film Avatar:

domenica 5 luglio 2015

191. La Curvatura degli Ombrelloni

Se le persone credono che la matematica non sia semplice, è soltanto perché non si rendono conto di quanto la vita sia complicata.

John von Neumann

La matematica è una scienza a buon mercato. A differenza della fisica o della chimica, non richiede di particolari attrezzature, basta osservare ciò che ci sta intorno, e qualche cosa su cui congetturare si trova sempre.

Dopo la sosta al bar, sono andato in spiaggia e una delle prime cose che ho notato è stata la particolare forma degli ombrelloni.

E’ da diversi anni che volevo scrivere un post sulla loro forma e questi ultimi mi hanno proprio fornito lo spunto che cercavo.

Claude Perrault (1613-1688) è stato un medico (di professione) e architetto (per diletto) francese. Morì per un'infezione contratta dopo aver sezionato un cammello.

Malgrado si ritenesse un architetto dilettante, a lui si deve la facciata est del Louvre di Parigi.

Terzo in una famiglia di sette figli, ebbe una formazione enciclopedica, con la naturale curiosità e lo spirito critico dello scienziato.

Il fratello Charles fu uno scrittore, autore del celebre libro di fiabe Contes de ma mère l'Oye (it. I racconti di Mamma Oca), raccolta di undici fiabe fra cui Cappuccetto Rosso, Barbablù, La bella addormentata, Pollicino, Cenerentola e Il gatto con gli stivali.

Uno dei problemi che si pose Claude Perrault, giocando con il suo orologio da taschino posto sul tavolo e provando a trascinarlo per la catenella fu:

se trasciniamo un oggetto posto su un piano orizzontale con una corda, quale sarà il percorso dell’oggetto se l’altro capo scorre lungo una linea retta situata sullo stesso piano?

Non riuscendo a risolvere il problema, lo pose quindi all'amico Leibniz (1646-1716) all'epoca del suo soggiorno a Parigi (1672-1676), la soluzione che consiste nella determinazione della curva, venne pubblicata nel settembre del 1693.

La proprietà geometrica caratteristica della curva, è dunque che, in ogni suo punto, il segmento di tangente compreso tra il punto stesso e la retta fissa ha lunghezza costante uguale alla lunghezza della corda. Da tale proprietà se ne deduce l'equazione differenziale.

Per essere precisi, Leibniz cominciò a studiare la curva del moto, ma fu Huygens che riuscì a definirla con precisione. La curva venne chiamata Trattrice (dal latino tractrix, che deriva a sua volta da trahere, trainare).

Una sua proprietà è di avere come evoluta una Catenaria.

Trattrice con oggetto posizionato inizialmente nel punto (4,0)

L’area compresa tra la Trattrice (con lunghezza L della corda) e il suo asintoto è:

La rotazione della Trattrice intorno al proprio asintoto genera la Pseudosfera, che deve il nome al fatto che la sua curvatura è costante in ogni punto e opposta a quella della Sfera:

k = -1/L²

Tale superficie fu proposta da Eugenio Beltrami (1835-1900) come modello di geometria iperbolica nel 1868.

Essa, infatti, localmente soddisfa gli assiomi della geometria iperbolica, allo stesso modo di come la superficie di un Cilindro localmente è un modello equivalente ad un piano euclideo o la Sfera uno di geometria ellittica.

E’ importante sottolineare che la Pseudosfera possiede una curvatura negativa costante, cioè, in maniera analoga alla Sfera (anche se meno evidente), in ogni suo punto si ha lo stesso valore di curvatura.

Un altro esempio è la superficie di Dini che può essere vista come una "torsione" della Pseudosfera. Più precisamente, è una superficie ottenuta assegnando a una Trattrice un moto elicoidale intorno alla propria retta caratteristica. È quindi una superficie elicoidale. Per confronto, la Pseudosfera è ottenuta facendo ruotare una Trattrice intorno alla propria retta caratteristica, ed è quindi una superficie di rotazione.
Come la Pseudosfera, la superficie di Dini ha curvatura gaussiana costante negativa.

Superficie e Volume della Pseudosfera sono rispettivamente:

Per la sfera invece si ha (come noto):

La geometria piana di Euclide si basa su 5 postulati.

Il più famoso di questi è il quinto postulato:

“per un punto esterno ad una retta, si può condurre una sola parallela alla retta”.

Senza entrare nei dettagli, possiamo dire che se non si accetta il quinto postulato, si hanno 2 alternative, alle quali corrispondono 2 diverse geometrie non euclidee:

1. “non si può condurre alcuna parallela” (geometria ellittica)

2. “si possono condurre almeno 2 rette parallele” (geometria iperbolica)

Si distinguono 2 tipi essenziali di curvatura:

· curvatura estrinseca: è la curvatura posseduta dall'oggetto in relazione ad uno spazio piatto di dimensione superiore in cui è immerso e determinabile solo confrontando elementi dell'oggetto in relazione ad elementi dello spazio contenitore;

· curvatura intrinseca: è la curvatura determinabile utilizzando solo operazioni eseguite su elementi dell'oggetto medesimo.

Un esempio di curvatura estrinseca è quella di una superficie cilindrica nello spazio tridimensionale: le linee tracciate sul cilindro sono curve se confrontate con le rette dello spazio in cui il cilindro è immerso. La geometria intrinseca del Cilindro è invece piatta, in quanto su di essa valgono tutti gli assiomi del piano euclideo.

Come si è detto, un Cilindro ha curvatura intrinseca nulla.

ANDY WARHOL, Campbell’s Soup II, 1969, screenprint on woven paper, 88.9 × 58.4 cm. Copyright the Andy Warhol Foundation for the Visual Arts. Courtesy the Andy Warhol Museum, Pittsburgh.

Questo può essere facilmente compreso, pensando che una etichetta di un barattolo non è altro che un foglio rettangolare arrotolato.

http://artasiapacific.com/Magazine/82/TheLittleCanThatCould

Una Sfera ha invece una curvatura intrinseca, determinabile rimanendo all'interno della superficie stessa: sulla Terra, un percorso che parte dal polo nord scendendo lungo un meridiano, ruota ad angolo retto lungo un parallelo e nuovamente ad angolo retto lungo un altro meridiano, ritorna al punto di partenza.

Mentre un percorso analogo eseguito su un piano non ripassa per lo stesso punto.

Tornando all’ombrellone, possiamo provare a scomporlo in figure geometriche semplici; procedendo dal basso verso l’alto avremo così:

· il telo giallo costituente la parte più importante, che può essere pensato come una calotta sferica, la cui curvatura è quindi positiva

· il secondo telo che sembra riprodurre una Pseudosfera (curvatura negativa)

· a seguire una parte cilindrica, una pseudosferica e una sferica.

Si vede quindi che nello stesso oggetto si possono trovare diverse tipologie di superfici.

http://www.vialattea.net/curvatura/index.html

Un altro modo per descrivere la Trattrice, è quella di considerare un cane che viene trascinato dal suo padrone tramite un guinzaglio, lungo un percorso rettilineo: il cane percorrerà una Trattrice.