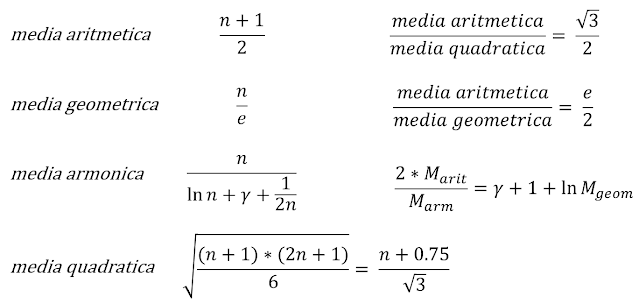255. Rapporti di medie

Supponete di prendere la media aritmetica e la media geometrica dei primi n numeri interi positivi.

Il rapporto delle due medie al crescere di n converge a e/2

Vediamo perché.

Dalla definizione delle medie matematiche (vedi post 200):

Media aritmetica - La media aritmetica viene calcolata sommando tutti i valori a disposizione e dividendo il risultato per il numero dei dati n.

Media geometrica - La media geometrica di n termini è la radice n-esima del prodotto degli n valori.

Quello che dobbiamo fare è di dimostrare questo limite:

    1 - La somma dei primi n numeri è n * (n+1) / 2 da cui (dividendo per n) segue che la media aritmetica è (n+1) / 2

    2 - Il prodotto dei primi n numeri è per definizione n! 

utilizzando l’approssimazione di Stirling  

e tenendo presente che, per n che tende a infinito, la prima parte della formula (che contiene la radice quadrata) tende a 1, la media geometrica tende a n/e.

Come volevasi dimostrare il rapporto tra le due medie è proprio e/2

Se si considerano anche altre medie:

Media armonica - La media armonica di n termini è definita come il reciproco della media aritmetica dei reciproci.

Media quadratica - La media quadratica di n termini è definita come la radice quadrata del rapporto tra la somma dei quadrati dei valori ed n.

con successioni di queste medie con n crescente si possono ottenere i seguenti rapporti:

Dove gamma è la costante di Eulero-Mascheroni

Zibaldone Scientifico: 163. Gauss & Faulhaber (zibalsc.blogspot.com)

Zibaldone Scientifico: 200. Media armonica (zibalsc.blogspot.com)

Zibaldone Scientifico: 203. Fattoriale, Fibonacci e Conigli (zibalsc.blogspot.com)

Zibaldone Scientifico: 253. Radici – parte seconda (zibalsc.blogspot.com)