Durante un viaggio può capitare di
chiedersi quanto tempo sarà necessario per arrivare a destinazione. Ad esempio
se dobbiamo percorrere 200 km e stimiamo una velocità di crociera di 100
km/ora, non è difficile capire che prevediamo 2 ore di viaggio.
Poi arrivati a metà percorso ci
accorgiamo che la velocita media è di soli 80 km/ora. E allora, se vogliamo
recuperare rispetto alla tabella di marcia, a quale velocità dobbiamo
percorrere la seconda metà del tragitto?
Ovviamente la risposta non è 120 km/ora,
altrimenti il post finirebbe qui.
Un’altra domanda potrebbe essere: se
andassimo ad 80 km/ora sino a metà percorso e 120 km/ora dopo, quale sarebbe la
velocità media?
Prima di rispondere alle 2 domande,
prendiamo in rassegna le 3 medie più utilizzate.
Media aritmetica
La media aritmetica è il tipo di media
impiegato più comunemente; quello al quale, con il termine "media",
si fa in genere riferimento. Viene usata per riassumere con un solo numero un
insieme di dati su un fenomeno misurabile (per esempio, l'altezza media di una
popolazione o il numero medio di figli per coppia).
Viene calcolata sommando tutti i valori
a disposizione e dividendo il risultato per il numero complessivo dei dati.
A volte alcuni elementi dell’insieme
preso in considerazione hanno come valore la media (considerando ad esempio
l’altezza degli italiani), mentre non ha senso dire che una coppia ha 1,4
figli.
Media geometrica
La media geometrica di n
termini è la radice n-esima
del prodotto degli n
valori.
Media armonica
La media armonica di n
termini è definita come il reciproco della media aritmetica dei reciproci. La
media armonica è fortemente influenzata dagli elementi di modulo minore.
In generale si ha: M aritmetica > M geometrica > M armonica
Inoltre per medie di 2 soli valori:
M
aritmetica : M geometrica = M geometrica
: M armonica
Prendiamo ad esempio i 2 valori 1 e 100, abbiamo rispettivamente:
Media aritmetica ( 1 ; 100 ) 50,5
Media geometrica ( 1 ; 100 ) 10
Media armonica ( 1 ; 100 ) 1,98
50,5
: 10 = 10 : 1,98
Torniamo ora al problema iniziale, cominciando
dalla seconda domanda:
se
andassimo ad 80 km/ora sino a metà percorso e 120 km/ora dopo, quale sarebbe la
velocità media?
La risposta è 96 km/ora.
Proviamo a verificarlo con un esempio:
se dovessimo percorrere 480 km, per i
primi 240 km ad 80 km/ora sarebbero necessarie 3 ore, mentre per gli altri a
120 km/ora basterebbero 2 ore; in totale 5 ore. Per cui 480 / 5 = 96 km/ora.
La media corretta è la Media armonica. Per 80 e
120 abbiamo infatti:
Media aritmetica ( 80 ; 120 ) 100
Media geometrica ( 80 ; 120 ) 97,98
Media armonica ( 80 ; 120 ) 96
100
: 97,98 =
97,98
: 96
La prima domanda chiedeva invece:
a quale velocità dobbiamo percorrere la
seconda metà del tragitto?
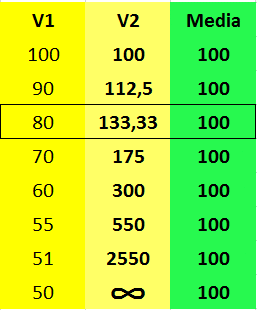
La risposta è 133,33 km/ora.
Infatti: Media
armonica ( 80 ; 133,33 ) 100
Coppie di velocità che hanno come Media armonica 100 sono riportate in
tabella:
Media
armonica deriva dal fatto che in uno strumento a
corda dimezzandone la lunghezza, la nota emessa raddoppia di frequenza e se
riduciamo la sua lunghezza ad un rapporto 2/3 otteniamo una quinta, che è
comunque in “accordo”.
Si dice che 1, 2/3 e 1/2 formano una
progressione armonica (musicale), partendo da un Do si arriva al Sol e quindi
al Do di un’ottava superiore.
Al passaggio successivo otterremmo 4/5 (terza),
nel nostro esempio un Mi.
La formula per calcolare la Media armonica ricorda il calcolo del
valore di resistenze poste in parallelo. Esiste anche un modo semplice per ottenere
il valore della Media armonica in
modo analogico:
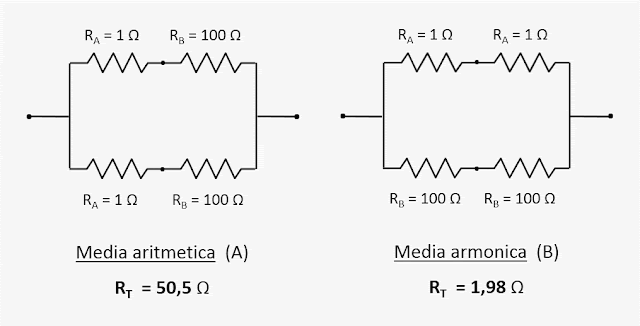
Per lo schema
A il
valore della Resistenza Totale RT è la Media aritmetica di RA
ed RB; mentre per lo schema B, RT rappresenta la Media armonica di RA ed RB.
Un esempio ingegnoso è rappresentato dal
seguente schema:
Per approfondire consiglio i seguenti post:
Nessun commento:
Posta un commento