Zibaldone Scientifico: settembre 2014

mercoledì 24 settembre 2014

164. Somma di Cubi

Il post precedente si concludeva con la bella formula:

1³ + 2³ + 3³ + … + n³ = (1 + 2 + 3 + … + n)²

La verifica è presto fatta. La somma dei cubi presenti nella parte sinistra abbiamo visto essere uguale a:

Mentre alla destra dell’uguale abbiamo il quadrato della somma dei primi n numeri:

Elevando alla seconda potenza questo risultato si ottiene facilmente la formula precedente.

Ma esiste anche in questo caso una semplice interpretazione grafica.

La somma dei cubi può essere riscritta come:

1³ + 2³ + 3³ + … + n³ = 1 x 1² + 2 x 2² + 3 x 3² + … + n x n²

La costruzione in figura mostra come con ad un primo quadratino di lato 1 si possono aggiungere 2 quadrati di lato 2 e continuando così 3 di lato 3, 4 di lato 4, ecc. Per essere precisi, i quadrati con lato pari vengono posizionati in modo che alle estremità vengano poste 2 metà.

http://users.tru.eastlink.ca/~brsears/math/oldprob.htm#s32

http://www.pinterest.com/ericc/proofs-without-words/

mercoledì 17 settembre 2014

163. Gauss & Faulhaber

Un famoso aneddoto racconta di come Johann Carl Friedrich Gauss (1777 - 1855), matematico, astronomo e fisico tedesco, all'età di 10 anni riuscì a stupire il suo insegnante di matematica (J.G. Buttner).

Un giorno che gli studenti erano particolarmente turbolenti, l’insegnante diede loro il compito di calcolare la somma dei primi 100 numeri (da 1 a 100) pensando così di tenerli impegnati per lungo tempo nell’eseguire un centinaio di somme. Dopo solo pochi minuti, il giovane Gauss gli pose sotto gli occhi il risultato corretto (5050).

Probabilmente, si era accorto che, mettendo in fila tutti i numeri da 1 a 100 e nella riga sottostante i numeri da 100 a 1, ogni colonna dava come somma 101; Gauss fece dunque il prodotto 100 x 101 e divise per 2, o più semplicemente 50 x 101 ottenendo facilmente 5050.

Wikipedia riporta che probabilmente Buttner aveva assegnato un compito ancora più complesso, ovvero la somma dei primi 100 numeri della serie 81297 + 81495 + 81693 ... nella quale ogni termine differisce dal precedente per il valore 198 e che il giovane Gauss lo risolse in pochi minuti come detto prima.

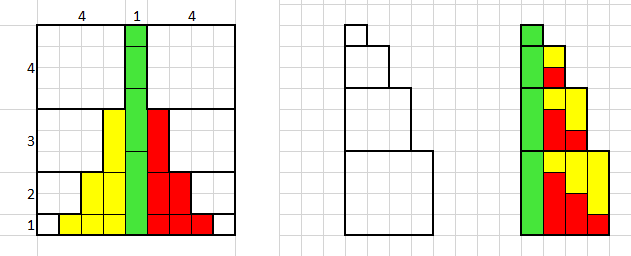
La seguente rappresentazione grafica mostra in modo semplice come sistemando i valori in modo opportuno si ottengono N colonne di valore N+1 e visto che ogni valore viene contato 2 volte, si deve alla fine dividere per 2, cioè:

N x (N+1) / 2

In questo caso si hanno 10 colonne di valore 11, per sommare i numeri da 1 a 10.

Al contrario di quello che normalmente si crede, questo risultato fu però ottenuto 150 prima (nel 1631) dal matematico Johann Faulhaber (1580 – 1635), che calcolò anche le somme delle potenze di interi successivi:

In questa e altre formule intervengono i numeri di Bernoulli B_n. Si osserva che la somma delle potenze m-esime dei primi n interi positivi è data da un polinomio di grado m+1. In effetti Carl Jacobi nel 1834 ha dimostrato che questa proprietà vale per tutti gli interi positivi.

Le singole formule possono essere ricavate per induzione o scrivendo sistemi di equazioni di grado m+1, risolvendole per sostituzione.

Ad esempio per la somma dei primi n interi ipotizziamo che il risultato sia del tipo:

a n² + b n + c

Sostituendo n con rispettivamente 0, 1 e 2 otteniamo:

                  c = 0
                       a + b + c = 1                >>>>>                 a + b = 1
                       4a + 2b + c = 3                                       4a + 2b = 3

da cui:

a = b = ½

e quindi la sommatoria risulta:

½ n² + ½ n + 0 = ½ n (n + 1)

Per la somma di quadrati e cubi abbiamo rispettivamente:

Mentre per le successive espressioni polinomiali prosegue:

Esistono anche rappresentazioni grafiche della somma di serie di quadrati o cubi.

Di seguito viene riportata la rappresentazione grafica della sommatoria dei primi n quadrati:

1² + 2² + 3² + 4²= 30

1² + 2²+ 3² + 4² + 5² = 55

Come si vede utilizzando 3 serie di quadrati, e combinandoli opportunamente, si ottiene un rettangolo i cui lati sono rispettivamente:

“la somma degli interi da 1 a n” e “(2 volte n) + 1”

L'area di ogni serie di quadrati è quindi: N x (N +1) x (2N + 1) / 6

Il 6 e’ dovuto al fatto che nella somma da 1 a n e’ presente 1/2 e l’area va divisa per 3 (numero di serie utilizzate).

Riporto infine un'altra formula notevole:

1³ + 2³ + 3³ + … + n³ = (1 + 2 + 3 + … + n)²

http://en.wikipedia.org/wiki/Euler%E2%80%93Maclaurin_formula

http://en.wikipedia.org/wiki/Bernoulli_numbers
http://www.robertobigoni.eu/Matematica/FTrascendenti/f08/f08.htm
http://it.wikipedia.org/wiki/Somma_di_potenze_di_interi_successivi
http://en.wikipedia.org/wiki/Faulhaber%27s_formula

lunedì 8 settembre 2014

162. Grandi Numeri

"Fa più rumore un albero che cade di una foresta che cresce"

Lao Tzu

Il tema di questo mese del Carnevale della Matematica, ospitato da Mr. Palomar, “Matematica mostruosa, spaventosa, vertiginosa” è molto stimolante per il fatto che diversi argomenti di matematica danno un certo senso di vertigine…

I frattali forniscono un esempio di come con continui ingrandimenti si riescano ad ottenere sempre nuove figure, anche se in qualche modo auto-simili, che danno la sensazione di precipitare in un pozzo senza fondo.

Insieme di Mandelbrot

Anche alcune comuni funzioni dotate di asintoti verticali, come le funzioni f(x) = 1/x oppure f(x) = tg(x), tendono all’infinito nell’intorno di alcuni valori, assumendo nel percorso qualsiasi numero: intero, razionale, irrazionale o trascendente che sia.

Ci sono però alcune funzioni che rendono bene il concetto di grandi numeri.

Knuth's up-arrow notation – l’idea è basata sul fatto che, in matematica, la moltiplicazione può essere vista come un’addizione iterata e la potenza come una moltiplicazione iterata. Alla stessa stregua iterando la potenza si arriva alla definizione di tetrazione:

^ba = (…(((((a^a)^a)^a)^a)^a)…)^a dove “a” compare “b” volte

Donald Knuth ha utilizzato la notazione freccia in su per la codifica, dove una freccia indica la potenza, due frecce la tetrazione, ecc.: + , x , ↑ , ↑↑ , …

All’interno de “Il libro dei numeri” John Horton Conway e Richard K. Guy definiscono numeri di Ackermann la sequenza:

1↑1 = 1¹ = 1

2↑↑2 = 2↑2 = 2² = 4
3↑↑↑3 = 3↑↑3↑↑3 = 3↑↑(3↑3↑3) = 3↑↑((3)³)³ = 3↑↑7625597484987
4↑↑↑↑4 = 4↑↑↑4↑↑↑4↑↑↑4 = …

Il terzo numero di Ackermann è ^{7625597484987}3 cioè (…((3³)³)…)³

dove “3” compare 7625597484987 volte.

Tralascio lo sviluppo del quarto numero, che potete trovare qui.

Ovviamente si possono definire numeri decisamente più grandi, come ad esempio il numero di Graham, considerato il primo numero di grandezza inconcepibile ad essere utilizzato in una seria dimostrazione matematica (riguardo ad un problema della teoria di Ramsey). Per un ulteriore approfondimento potete anche consultare un post del 2013 dell'ospite di questo Carnevale o quello del 2012 di mau.

D’altro canto se pensiamo alle dimensioni o all’età dell’Universo ci rendiamo conto che i numeri in gioco sono più contenuti.

Per chi volesse festeggiare il proprio primo miliardesimo secondo, un miliardo di secondi corrisponde a poco più di 31 anni e mezzo. L’età dell’Universo (espressa in secondi) è rappresentata da una cifra con “solo” 17 zeri; come dire che volendo contare il numero di atomi contenuti in un milligrammo di materia a partire dal Big Bang, si dovrebbe tenere un ritmo di almeno 100 atomi/secondo.

Quello che abbiamo visto sino ad ora tratta di “grandi numeri” che crescono molto velocemente. Ma non bisogna dimenticare che qualsiasi funzione che cresca in modo monotono, raggiunge e supera, prima o poi, questi valori.

Si potrebbe continuare accennando alla Teoria degli Insiemi sviluppata da George Cantor; dove, oltre che ad insiemi finiti, si fa riferimento ad insiemi infiniti, come

N = {0, 1, 2, 3, 4, ...} che contiene “tutti” i numeri naturali, ma non “tutti” i numeri reali (che avendo una cardinalità maggiore) sono di un altro tipo di infinito. Ma Cantor non si è accontentato di questo e ha fornito un metodo per costruire insieme infiniti sempre più grandi.

La citazione di Lao Tzu fatta all’inizio, diventata famosa anche per essere stata riportata su molte magliette o negli incipit di parecchi libri, serve a ricordare come nella matematica che si impara durante un normale corso di studi siano contenuti concetti mostruosi, spaventosi e vertiginosi, che crescendo con noi facevano poco rumore.

Lao Tzu è una figura leggendaria della filosofia cinese. La tradizione tramanda che sia vissuto nel VI secolo a.C. ed è considerato il fondatore del Taoismo.

Alcuni affermano che un giorno abbandonò le sue attività e intraprese un viaggiò verso Occidente con il suo bufalo, attraverso lo Stato di Qin. Arrivato al posto di guardia di Hangu, Lao Tzu fu interpellato da un ufficiale, il quale gli chiese di lasciare qualche scritto sulla sua filosofia prima di andarsene. La risposta di Lao Tzu all'ufficiale furono i cinquemila ideogrammi del Tao Te Ching, la prima e unica opera scritta del filosofo.

Lao Tzu lasciò il suo testo su tavolette di bambù al guardiano.

Fatto questo ripartì e scomparve nelle distese desertiche senza essere mai più visto.

Tratto da: http://it.wikipedia.org/wiki/Laozi