Nel numero di dicembre 2016 della
rivista “Le Scienze”, Piergiorgio
Odifreddi ci parla dell’arte di
sbagliare i calcoli, ed in particolare distilla diverse idee riguardanti
analisi delle probabilità e statistica. Non ripeterò qui quanto descritto nell’articolo, ma prenderò spunto da questo
per un paio di post.
Primo dei due post:
Jean Paul de Gua de Malves (Carcassonne, 1713 –
Parigi, 1785) è stato un abate, matematico ed economista francese. Gua de
Malves era pienamente introdotto nell'ambiente dei filosofi francesi durante
l'ultimo periodo dell'Ancien Régime e fu uno dei primi scienziati coinvolti
nella compilazione dell'Encyclopédie,
della quale fu coordinatore principale dal 1745 al 1747, quando il suo posto fu
preso da Denis Diderot.
Pitagora
(Samo, 570 a.C. circa – Metaponto, 495 a.C. circa) è stato un filosofo greco.
Quasi sicuramente non lasciò nulla di scritto e anche le opere a lui ascritte,
vanno attribuite ad autori sconosciuti, che vissero in epoca cristiana o di
poco antecedente. Pitagora è considerato l'iniziatore del vegetarianismo in
Occidente grazie ad alcuni versi delle Metamorfosi
di Ovidio, che lo descrivono come il primo degli antichi a scagliarsi contro
l'abitudine di cibarsi di animali, reputata dal filosofo un'inutile causa di
stragi, dato che la terra offre piante e frutti sufficienti a nutrirsi. Il teorema per cui il filosofo è famoso
era già noto agli antichi Babilonesi ed era conosciuto anche in Cina e in India,
ma alcune testimonianze riferiscono che Pitagora ne avrebbe intuito la
validità.
Enunciato:
in ogni
triangolo rettangolo il quadrato costruito sull'ipotenusa è sempre equivalente
all'unione dei quadrati costruiti sui cateti.
Il teorema di Pitagora si incontra in
qualsiasi ambito della matematica e della fisica. La sua dimostrazione è
abbastanza semplice ed intuitiva.
 |
| https://en.wikipedia.org/wiki/Pythagorean_theorem |
Una sostanziale generalizzazione del
teorema di Pitagora a 3 dimensioni è il teorema di de Gua:
se un
tetraedro ha un vertice formato da angoli retti (come nel caso dei vertici di un cubo), allora il quadrato
dell'area della faccia opposta a detto vertice è uguale alla somma dei quadrati delle aree
delle altre 3 facce.
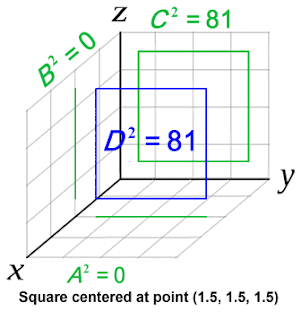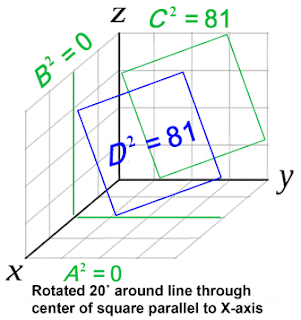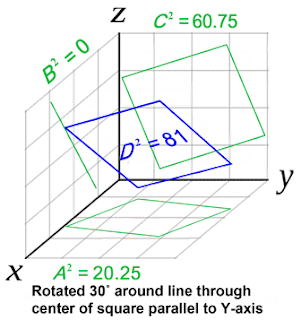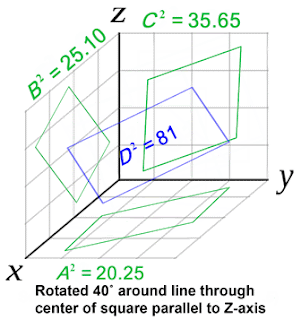
Esempio: si voglia calcolare l’area del
triangolo ABC di Figura 1 (dove i punti A, B e C, non hanno necessariamente lo
stesso valore). Se invece prendiamo 3 punti posizionati a distanza unitaria
dall’origine, ognuno dei 3 triangoli ha area 0,5, mentre il triangolo ABC
misura 0,866 (radice di 3, fratto 2).
Un'altra generalizzazione del teorema di Pitagora, introdotta da Donald R. Conant e William A. Beyer, si applica a una vasta gamma di oggetti e insiemi
di oggetti in qualsiasi numero di dimensioni.
Mi piace pensare che la nostra sia una
visione limitata del problema e che in realtà il teorema di Pitagora sia un
caso molto particolare di un teorema con validità molto più ampia.